Chapter 1: Budget Constraint End of Chapter Exercises
#1: Emma’s income is $25 and the price of cookies (x) is $2 per unit and the price of coffee (y) is $5.
a. Write down Emma’s budget constraint.
b.What is her price ratio?
c. If the price of cookies rises to $5 per unit and the price of coffee rises to $10, describe the new budget constraint
a. Steeper than the previous one and lies below it
b. Steeper than the previous one and lies above it
c. Flatter than the previous one and lies below it
d. Flatter than the previous one and lies above it
e. None of these are correct
#2: Examine a consumer's budget constraint with the following conditions: The consumer has $30 available to spend and there are two goods, x and y. While the p_y = 2 no matter what, the price of good $x$ is governed by the following scheme: The consumer has a coupon that reduces the price of the first six (6) units down to $1 but the consumer pays full price of p_x = 3 for all subsequent units.
Sketch the budget constraint. What is the maximal amount of good x that the consumer can afford?
Sketch of solutions:
#1a: Px = 2 and Py=5 while M=25, hence 2x+5y=25 is the BC.
#1b: Price ratio is Px/Py = 2/5
#1c: A is correct, steeper than the previous and lies below it. The price ratio is now 1/2 which is steeper than 2/5 (because 0.5 > 0.4). Lies below it follows because previous the vertical intercept was y=25/2 = 12.5 and now it’s y=25/5 = 5 and the horizontal intercept used to be x=25/5 = 5 and now is x=25/10 = 2.5.
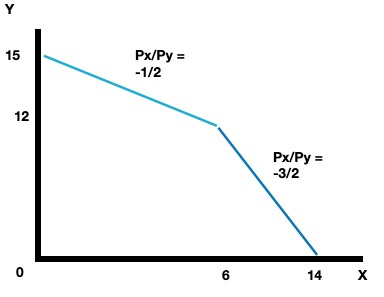
#2: Start by marking down the vertical intercept. It will be at (0,15). Then find the ‘kink’ point. The consumer reaches the kink when purchasing 6 units of good X. At that point the consumer will have $24 remaining and can purchase 12 units of Y or 8 units of X. The point (6,12) gives us the ‘kink’. The budget constraint will have a slope of -1/2 from the vertical intercept down to the kink and of -3/2 from the kink down to the horizontal intercept (14,0).